My house's pool in NorCal has a pool that gets a ton of shade from a row of about 6 redwoods that line the southern edge of property. It really shortens the swimming season and I've been trying to figure out how to extend it without having to run my gas heater so much ($$$). I was told adding a heat pump might be a good solution especially if I solar panels/battery to the home which gets great sun as its beyond the reach of the redwood's shade. The temps still drop down into the 40's and 50's some nights, especially in the shoulder months, so I'm trying to figure out if the heat pump running only during sunlight hours is going to be enough to get my temps up to swim by midday. I'm open to other ideas as well, to improve the economics such as solar panels for the pool itself by building a pool shed over the existing equipment (not sure I'd have space to put it otherwise). I already have an automatic pool cover.
Thinking about adding a heat pump if I'm planning on adding solar panels/battery to home
- Thread starter rpk1430
- Start date
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
- May 3, 2014
- 62,616
- Pool Size
- 6000
- Surface
- Fiberglass
- Chlorine
- Salt Water Generator
- SWG Type
- Pentair Intellichlor IC-40
Do you use a solar cover on the pool?
EDIT— I see an auto cover
As long as you keep it closed at night the pool should retain any heat added.
EDIT— I see an auto cover
As long as you keep it closed at night the pool should retain any heat added.
Ignoring the solar component, how big is the pool, and how big is the heat pump.
It really becomes a question of time vs heating capacity - Can you replace the overnight loss by the time you want to swim....
It really becomes a question of time vs heating capacity - Can you replace the overnight loss by the time you want to swim....
It’s 22,000 gallon. I saw that a heat pump is rated at 140,000 BTU. A pool guy told me that heat pumps are not great for my area because of low humidity, something about how the heat pump requires humidity to work efficiently. Most days I probably don’t start swimming until noon.
Last edited:
Humidity makes a difference.A pool guy told me that heat pumps are not great for my area because of low humidity, something about how the heat pump requires humidity to work efficiently
At 80% Humidity (80, 80, 80), the output is 145,000 btu/hr.
At 63% Humidity (80, 63, 80), the output drops to 135,000 btu/hr.
So, the heating output difference is about 10,000 btu/hr for a 17% humidity difference.
When water evaporates, it cools things down like when people sweat.
Conversely, when water condenses, heat is transferred to the surface where the water condenses.
It is basically the same amount of heat either way.
It is about 1,000 btu per pound of water.
Each pound of 80°F water that evaporates takes 1,048 BTU of heat out of the pool.
Each pound of water that condenses provides 1,048 BTU of heat to the heat pump.
Water condensation = Heat energy / Latent heat of condensation
Water condensation = 10,000 BTU/hr ÷ 970 BTU/lb
Water condensation = 10.31 pounds of water per hour
Converting to more common units:
10.31 pounds of water is approximately 1.24 gallons per hour
This equals about 4.68 liters per hour
Or about 78 milliliters per minute
This means the heat pump operating at 80% RH versus 63% RH is condensing approximately an additional 10.3 pounds (1.24 gallons) of water per hour from the air, which accounts for the 10,000 BTU/hr increase in heating capacity.
Water condensation = 10,000 BTU/hr ÷ 970 BTU/lb
Water condensation = 10.31 pounds of water per hour
Converting to more common units:
10.31 pounds of water is approximately 1.24 gallons per hour
This equals about 4.68 liters per hour
Or about 78 milliliters per minute
This means the heat pump operating at 80% RH versus 63% RH is condensing approximately an additional 10.3 pounds (1.24 gallons) of water per hour from the air, which accounts for the 10,000 BTU/hr increase in heating capacity.
80 Air, 80 Water and 0% humidity = 97,941 btu/hr
80 Air, 80 Water and 100% Humidity = 156,765 btu/hr.
Difference = 58,824 btu/hr.
That is about 60.64 lb of water or about 7.2 gallons of water difference.
Each 1% of humidity makes about 588 btu/hr of difference.
Note: Assumes that the equation is correct, but I am not sure that it is.
80 Air, 80 Water and 100% Humidity = 156,765 btu/hr.
Difference = 58,824 btu/hr.
That is about 60.64 lb of water or about 7.2 gallons of water difference.
Each 1% of humidity makes about 588 btu/hr of difference.
Note: Assumes that the equation is correct, but I am not sure that it is.
Last edited:

y = 588.24X + 97941, y from 97941 to 160000 - Wolfram|Alpha
Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.
The average annual relative humidity in Napa, California is 57.8%.
The relative humidity fluctuates throughout the year, with the highest humidity in January at 77% and the lowest in October at 50%.
In June, the average relative humidity is 56%, which is considered comfortable.
A Heat pump should work ok for you.
The relative humidity fluctuates throughout the year, with the highest humidity in January at 77% and the lowest in October at 50%.
In June, the average relative humidity is 56%, which is considered comfortable.
A Heat pump should work ok for you.
Water temperature = 85 degrees and pool covered.
Humidity = 63%.
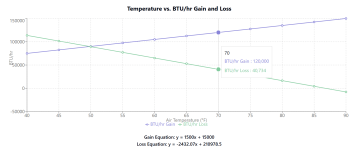
The equation for the Btu/hr gain line is: y = 1500x + 15000
The equation for the Btu/hr loss line is: y = -2432.07x + 210978.5.
X = Air Temperature.
Y = Btu/Hr.
50 degrees is the breakeven.
Above 50 degrees, the gain is higher than the loss and you can calculate Heat Pump runtime by Loss/Gain..
For example, at 70 degrees air, the gain is 120,000 btu/hr and the loss is 40,734, which is 34%.



Humidity = 63%.
The equation for the Btu/hr gain line is: y = 1500x + 15000
The equation for the Btu/hr loss line is: y = -2432.07x + 210978.5.
X = Air Temperature.
Y = Btu/Hr.
50 degrees is the breakeven.
Above 50 degrees, the gain is higher than the loss and you can calculate Heat Pump runtime by Loss/Gain..
For example, at 70 degrees air, the gain is 120,000 btu/hr and the loss is 40,734, which is 34%.






1500x + 15000 = -2432.07x + 210978.5, x from 35 to 100 - Wolfram|Alpha
Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.
The way I see it, it boils down to your perspective of the +/- of the equation. Are you a 'YAY it worked 2/3 of the time at a steep discount so I will happily eat the 1/3 it didn't work' or is the 1/3 of the time going to put you in a foul mood about it during the 2/3 of the time ?
We found it was more disappointing in the early season because it was new and exciting again when the weather was unfavorable for the HP. On cool years in the late season, nobody wanted to swim when the heat pump either didn't do great, or not at all. The last several years have broken records everywhere being much warmer. Had you had a HP in this stretch, you'd probably think they were awesome.
On warm years it'll be awesome. On average years it'll likely still sit well with you and on cool years only you can decide if you still like the big picture of things.
We found it was more disappointing in the early season because it was new and exciting again when the weather was unfavorable for the HP. On cool years in the late season, nobody wanted to swim when the heat pump either didn't do great, or not at all. The last several years have broken records everywhere being much warmer. Had you had a HP in this stretch, you'd probably think they were awesome.
On warm years it'll be awesome. On average years it'll likely still sit well with you and on cool years only you can decide if you still like the big picture of things.
They have gas heating, so that can make up the difference.
If they get solar power and the electricity is basically free, then that makes it an easy decision.
If you can sell back power, then you can consider the lost revenue of power used vs. sold back.
Overall, I think that it will be a good choice to get a 140,000 btu/hr heater.
If they get solar power and the electricity is basically free, then that makes it an easy decision.
If you can sell back power, then you can consider the lost revenue of power used vs. sold back.
Overall, I think that it will be a good choice to get a 140,000 btu/hr heater.
The equation relating water temperature (X) and heat loss (Y) is:
Y = 2400X - 132000.


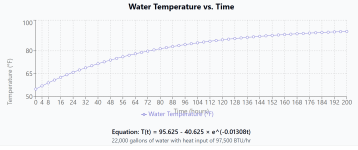
X(t) = 95.625 - 40.625 × e^(-0.01308t).
X(t) is the temperature in °F at time t.
t is time in hours

Formula: t = -ln((95.625 - T)/40.625)/0.01308
Where T is the target temperature in °F and t is time in hours
Y = 2400X - 132000.

| Temperature (°) | Heat Loss (BTU/hr) |
|---|---|
| 55 | 0 |
| 60 | 12,000 |
| 65 | 24,000 |
| 70 | 36,000 |
| 75 | 48,000 |
| 80 | 60,000 |
| 85 | 72,000 |
| 90 | 84,000 |

X(t) = 95.625 - 40.625 × e^(-0.01308t).
X(t) is the temperature in °F at time t.
t is time in hours


Time Required to Reach Target Temperatures
22,000 gallons of water with 97,500 BTU/hr heat input| Temperature (°F) | Time (hours) | Time (days) |
|---|---|---|
| 55 | 0.00 | 0.00 |
| 56 | 1.91 | 0.08 |
| 57 | 3.86 | 0.16 |
| 58 | 5.87 | 0.24 |
| 59 | 7.92 | 0.33 |
| 60 | 10.04 | 0.42 |
| 61 | 12.22 | 0.51 |
| 62 | 14.46 | 0.60 |
| 63 | 16.77 | 0.70 |
| 64 | 19.15 | 0.80 |
| 65 | 21.60 | 0.90 |
| 66 | 24.14 | 1.01 |
| 67 | 26.77 | 1.12 |
| 68 | 29.48 | 1.23 |
| 69 | 32.30 | 1.35 |
| 70 | 35.23 | 1.47 |
| 71 | 38.27 | 1.59 |
| 72 | 41.44 | 1.73 |
| 73 | 44.75 | 1.86 |
| 74 | 48.21 | 2.01 |
| 75 | 51.83 | 2.16 |
| 76 | 55.63 | 2.32 |
| 77 | 59.62 | 2.48 |
| 78 | 63.84 | 2.66 |
| 79 | 68.31 | 2.85 |
| 80 | 73.05 | 3.04 |
| 81 | 78.11 | 3.25 |
| 82 | 83.52 | 3.48 |
| 83 | 89.35 | 3.72 |
| 84 | 95.66 | 3.99 |
| 85 | 102.54 | 4.27 |
Where T is the target temperature in °F and t is time in hours
| Time (hours) | Temperature (°F) |
|---|---|
| 0 | 55.00 |
| 10 | 59.98 |
| 20 | 64.35 |
| 40 | 71.55 |
| 60 | 77.09 |
| 80 | 81.36 |
| 100 | 84.64 |
| 150 | 89.91 |
| 200 | 92.66 |
TFP is a registered 501(c)3 non-profit that is maintained by user donations.
The people who answer questions are volunteers.
If you find the site to be a good resource, please consider making a donation to help support the site.
Thanks.

 www.troublefreepool.com
www.troublefreepool.com
The people who answer questions are volunteers.
If you find the site to be a good resource, please consider making a donation to help support the site.
Thanks.

Become a TFP Supporter
Help Support TFP Trouble Free Pool is run by a dedicated group of volunteers that … Read more…






