I do get your point with different acid concentrations, as online calculators usually only offer to pick from acid strengths that are commonly available in the US. The unit systems can typically be adjusted, but you need a manual correction for the acid strength. In Australia, Hydrochloric Acid is usually labeled in the range 32%-34%.
OK, let's tackle that from the roots.
Lets start with the first conversion, changing the acid concentration. This is a bit tricky if doing it precisely, because the percentage on the acid bottle is not a volume percentage, but a mass percentage. For example, 32% HCl solution means that you have 0.32 kg of HCl per 1
kg of watery solution in that acid bottle. You have to divide that by the density of the HCl solution (for example 1.16kg/l for 32% HCl) to turn that into kg HCl per 1
litre of watery solution in the bottle.
Let's call V₁ the required volume of acid with percentage c₁ and density ρ₁, and V₂ the required volume of acid with percentage c₂ and density ρ₂ to achive the same pH change in the same volume of pool water.
To have mass equality of added HCl molecules, you have V₂ x (c₂/ρ₂) = V₁ x (c₁/ρ₁),
which gives you V₂ = V₁ x (c₁/ρ₁) / (c₂/ρ₂).
If the concentrations c₁ and c₂ aren't too different, then you can neglect the difference in densities, and simplify that to
V₂ = V₁ x c₁ / c₂
Now, conversion 2, we add units and want V₁ in oz, and V₂ in ml:
V₂[ml] = V₂[oz] x 29.5735ml/oz = V₁ x c₁ / c₂ x 29.5735ml/oz
Let's move on to conversion 3, and assume that V
1,10kG[oz] is the required acid addition for 10000gal of water which is 10000gal x 3.785412l/gal = 37854.12l. To turn that into V
1,10kL[oz] (the required acid addition, still in oz, for 10000l of water), you have to divide therefore by 3.785412l/gal.
Everything put together:
V
2,10kL[ml] = V
1,10kG[oz] x c₁ / c₂ x 29.5735ml/oz / 3.785412l/gal
Which confirms what you had, under the assumption that the differences in acid density can be neglected.
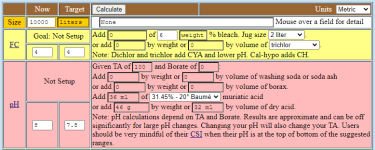
Let's get an example, and calculate with the online
PoolMath calculator the required volume [oz] of 31.45% MA for a pH change from 8.0 to 7.8 for 10000gal of water with TA 100:

To turn that into the required volume [ml] (still for 31.45% MA) per 10000l of water, we multiply with 29.5735 and divide by 3.785412, and get 35.94ml. With PoolMath we get 36ml, our formula seems to be in agreement:
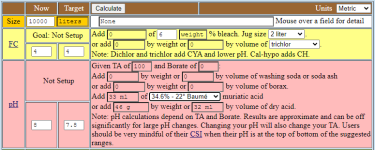
Now we want to use 34.6% acid (just to pick an example that is available in the calculator to check our formula). We have to multiply with 31.45 and divide by 34.6, and get 32.67ml. PoolMath gives us 33ml, calculation seems to be right:
My recommendation would be to use the
PoolMath online calculator or the
PoolMath app (if you are just interested in calculations and no data logging, you don't need to pay), and then just do the concentration adjustment manually. Or just ignore the small difference between the nearest concentration on offer and what you actually need.




